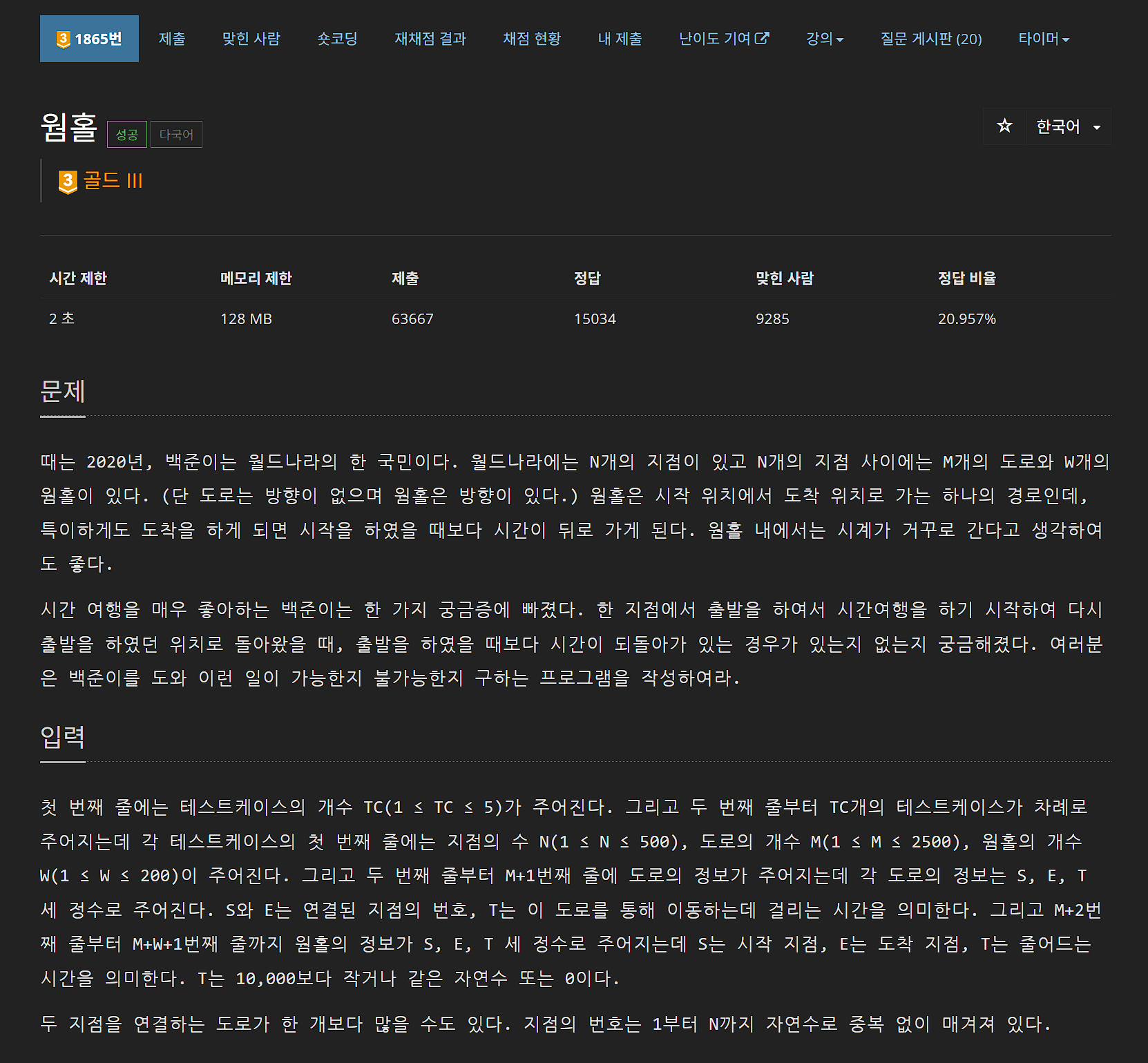
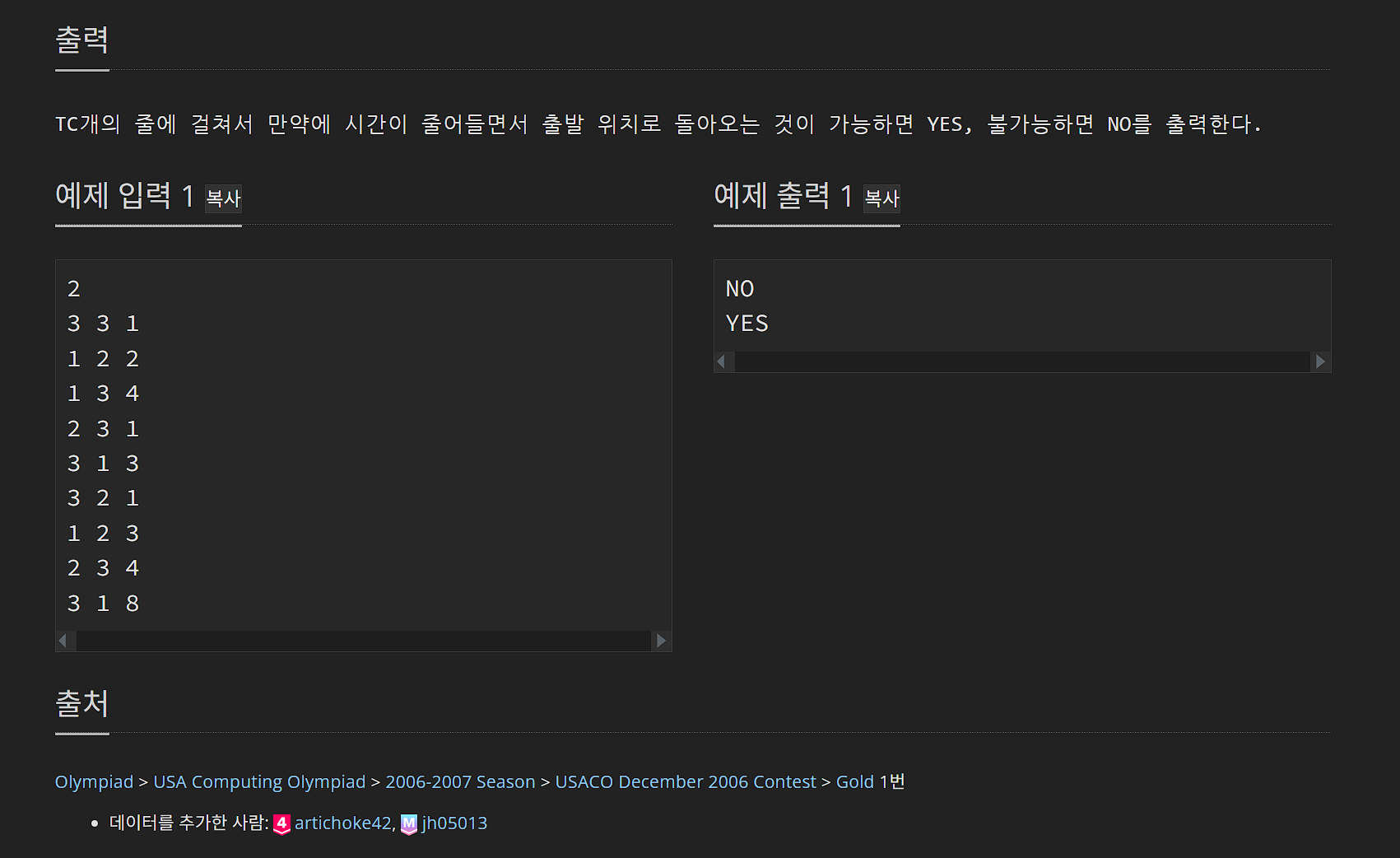
[BOJ1865 웜홀] 음수사이클 탐지 목적으로 벨만 포드 변형하기

boj1865 웜홀 문제

https://www.acmicpc.net/problem/1865

잡아야 할 포인트

• 도로는 양방향 간선
• 웜홀은 음수 가중치를 가지는 단방향 간선
• 출발 노드와 도착 노드가 같을 때만 고려함

세 번째가 중요하다. 문제 지문을 보면 아래와 같은 내용이 있다.

한 지점에서 출발을 하여서 시간여행을 하기 시작하여 다시 출발을 하였던 위치로 돌아왔을 때, 출발을 하였을 때보다 시간이 되돌아가 있는 경우가 있는지 없는지 궁금해졌다.

머리를 써서 해석해보면,

“음수cycle이 존재한다면 YES, 존재하지 않는다면 NO 출력”

과 똑같은 말이다.

음수cycle만 판별하는 효율적인 알고리즘?

벨만 포드만 사용할 경우 문제점

벨만 포드는 시작 정점을 두고 작동하는 알고리즘이다. 따라서 비연결그래프에서 벨만 포드를 돌리면 시작 정점과 연결된 그래프의 음수cycle 존재 여부만 감지할 수 있다.

이를 해결하기 위해서는 모든 정점을 시작 노드로 한 번씩 잡고 n(정점의 수)만큼 벨만 포드를 반복할 수도 있다.

하지만 시간 초과가 날 것이다…. (내가 그랬다.)

해결 방법 - 가상의 0번 노드 만들기

기존 벨만 포드 알고리즘을 그대로 적용하되, 한 가지 아이디어를 추가했다.

가상의 0번 노드를 만들고, 0번 노드에서 각 노드를 가리키는 단방향 간선을 추가하는 것이다.

(0번 노드에서 나가는 간선만 있으므로, 의도하지 않은 cycle은 당연히 발생하지 않는다.)

// 가상의 0번 노드와 모든 정점 연결하기!
for(int i=1; i<=N; i++) {
	edges.push_back({0, i, 0});
}

정답 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <limits.h>
#include <tuple>

using namespace std;
using ll = long long;

typedef tuple<int,int,int> edge;

int N, M, W, TC;

int main() {
    ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int u, v, w;
	cin >> TC;

	for(int t=0; t<TC; t++) {
		vector<edge> edges;
		vector<long> dist;
		// cout << "testcase: " << t << endl; // for test
		cin >> N >> M >> W;
		// dist 배열 초기화
		dist.resize(N+1);
		fill(dist.begin(), dist.end(), LONG_MAX);
		for(int i=0; i<M; i++) {
			cin >> u >> v >> w;
			edges.push_back({u, v, w}); // 양방향 간선
			edges.push_back({v, u, w});
		}
		for(int i=0; i<W; i++) {
			cin >> u >> v >> w;
			edges.push_back({u, v, (-1)*w}); 
		}
		// 가상의 0번 노드와 모든 정점 연결하기!
		for(int i=1; i<=N; i++) {
			edges.push_back({0, i, 0});
		}
		
		bool checkCycle = false;	
		dist[0] = 0; // 가상의 0번 노드를 시작으로
		for(int i=0; i<N; i++) {
			for(int j=0; j<edges.size(); j++) {
				edge tmp = edges[j];
				u = get<0>(tmp);
				v = get<1>(tmp);
				w = get<2>(tmp);

				if(dist[u]!=LONG_MAX && dist[v] > dist[u] + w) {
					dist[v] = dist[u] + w;
				}
			}
		}

		// 음수사이클 존재? -> 무조건 YES
		for(int j=0; j<edges.size(); j++) {
			edge tmp = edges[j];
			u = get<0>(tmp);
			v = get<1>(tmp);
			w = get<2>(tmp);

			if(dist[u]!=LONG_MAX && dist[v] > dist[u] + w) {
				// cout << "negative cycle!!" << endl; // for test
				checkCycle = true;
				break;
			}
		}		
		if(checkCycle == true) cout << "YES\n";
		else cout << "NO\n";
	}
}